Interactive Dice Test Probability Webpage

[Telnoratti]

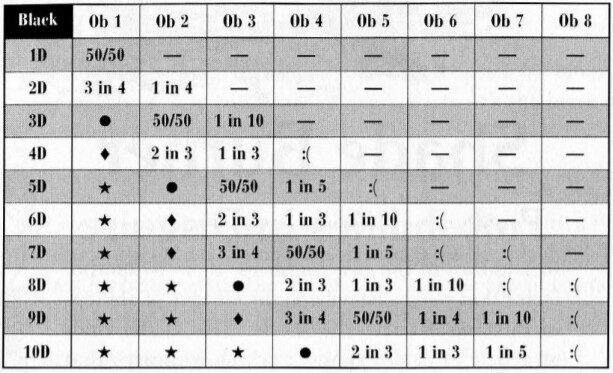
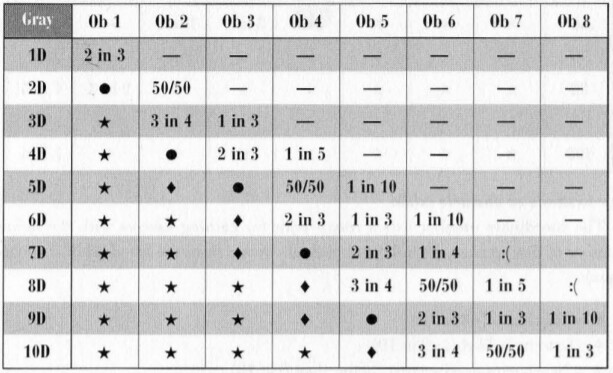
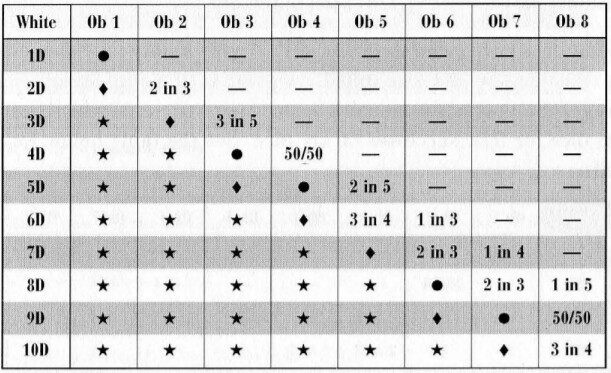
Here’s the link: https://burningwheel-dice.herokuapp.com/

I’m getting ready to start a BW campaign with my regular TTRPG group. They loved the one-shot I ran for them, but they’ve been asking me questions about how different ways to spend Artha on a roll will help and if it’s “worth it”. Also as a new GM I’m having a hard time setting obstacles (though the discussion in the Codex was very helpful). I put together a little dashboard for myself so that I could understand how likely a roll is to succeed and so my players and myself understand how and when to spend Artha.

This is not a dice simulator, so it will be exact and relatively fast. I solved for the probabilities using sympy. It’s been 8 years since I’ve worked with generating functions, so it’s possible I made mistakes. I double checked my work against simulations and it seems to all check out. Obviously I have not checked every combination, but I did test several different scenarios. Please let me know if you find math errors or rule interpretation errors.

If anyone is interested, I actually solved the more general problem for more dice types (d20, d4, etc.) and exploding on more than just the maximum value. The code for the dashboard and solving is at https://github.com/telnoratti/burningwheel-tools. The ability to re-roll failures is on the way, but I haven’t solved it yet.

I know there are a couple of visual issues, but it’ll be a few days before I can work on it again. It was at the point that it may be useful to others, so I went ahead and set it up to share. I’d love feedback if anyone has ideas on how to make it more useful or intuitive. I was planning on sharing it with my players later this week at our kickoff session.

[luke (Luke Wheel)]

This is amazing. Very well done.

Can you walk me through your function regarding spending fate points for open-ending?

[Telnoratti]

Thanks, it was pretty fun to build and I got to justify spending work time on it since I was learning dash.

I’m not sure how much detail you’d like me to go into, but I’m using generating functions to do this. They basically take advantage of the fact that multiplying polynomials works the same way as calculating probabilities, but are a lot easier to write and work with once you wrap your head around them. The heart of this is in these lines of the code.

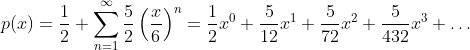The function I used for a single die of open-ended black shade skills is . The coefficients of x^n correspond to the probability of n successes. For example x^0 is 1/2, so there’s a 50% of getting 0 successes (rolls of 1, 2, or 3). The coefficient of x^1 is 5/12, which corresponds to a roll of 4 or 5, or a 6 when the exploded die rolls a 1, 2, or 3 the probability of this is 1/2 (2/3 + 1/3 * 1/2). I actually calculate the second and third terms in the code.

p_1 = success_chance*(dud_chance + explode_chance*failure_chance)
p_2 = success_chance*explode_chance*success_chance*(dud_chance + explode_chance*failure_chance)

success_chance and failure_chance are 1/2 for black shade skills, explode_chance is 1/3 because it’s the probability of a success exploding, and dud_chance is 2/3. The series is infinite and has non-zero values for arbitrarily high successes. This is because you could theoretically roll any number of sixes, however unlikely, before rolling something besides a 6 and there is a small chance of rolling an arbitrary number of successes.

Now that we have a polynomial whose coefficients correspond to probabilities of one die, getting the odds of multiple dice is just multiplying the polynomial by itself. This does the hard work of tracing out every path to get to, for example, 6 successes whether it’s by rolling six 4s or a 6, five 4s, followed by four 6s and a 4 from exploding dice. I used the sympy library to do the multiplication. Then I just checked the coefficients up to x^10 (Ob 10).

I use this same method for non-open-ended (…closed-ended?) tests as well. There the equation is just failure_chance + success_chance*x. There are easier ways to do it, but I was already doing it for the exploding dice. I haven’t yet done anything with re-rolling failures like Luck on an open-ended skill, Saving Grace, or Call-On Traits. That’s next.

[moconnor8 (Michael)]

Very impressive project with a clean, legible design. Well done!

[BeginnersLuck]

This is really great!

It’s probably just a rounding difference, but when the skill exponent is 3, Ob 1 is listed as 88% for Basic and 87% for Open-ended.

[Telnoratti]

It’s probably just a rounding difference, but when the skill exponent is 3, Ob 1 is listed as 88% for Basic and 87% for Open-ended.

Huh, so it does, excellent catch. The value for the basic one is 7/8 which is exactly 0.875. The value I calculated for open-ended is 1547517394171232587339775/1768591313891965945239551 which is 0.8749999968991… That’s a lot of 9s. This is all arbitrary precision, so it’s not a rounding issue. Rather it’s an issue with how I handled higher order terms. It’s fixed now, but I didn’t account for rolling more than 10 6s in a row on a single die. I now account for an infinite number of 6s in a row on a single die. Also included 3 decimal points in the hover text as I thought that may have been useful when seeing something odd like that.

[wateralmond]

EXCELLENT work with a very clear explanation

(I wish you had been my probability & statistics professor!)

[Telnoratti]

Thanks! I was surprised there wasn’t more about this method for exploding dice when I was searching since there are quite a few popular systems that use it. Hopefully the explanation on the site is thorough enough for people to adopt it to other systems.

[TheFarSeeing (Sean Hansen-Romu)]

I solved something related (only black exponent) for Torchbearer using recursion in excel, for the non-exploding case.
Here is a pic of the chart I made for my players: Chart image. I only used 1/2 chance of success per die and probability/combinitorics.

Here is the open office version.
Open Office/Excel File

I use this base chart, with some simple instructions to my players so they can estimate if it is worth rolling as is or using a trait against themselve, or if using Rewards are worth it. Persona just added to your die roll, prior to the fact. And Fate and rerolls are calculated as a seperate roll.

The way I handle rerolls on the chart is after the fact. So say you roll 6 dice against Ob5 and you get 3 success. and you get 3 dice to re-roll (reroll fails) and need 2 more successes. You simply consult the chart again to see if it its worth it.3D against Ob 2. This gives you a 50% chance of succeeding, at this point here and now. Since re-rolls are done after the fact, I never needed to calculate the odds of spending it before.

Similarly, there is a very rough estimate for spending Fate to explode 6s. You count them after the fact and compare them with how many extras you need. You consult the chart again. Say 4 sixes and you need 3 more successes. This means that Fate was worth a 31% chance of success, at the least. I never calculated the open-ended case, but my gut told me each die was an extra percent or two per die. An off the cuff estimate, I would say 31[base odds]+4[amount of dice]1[extra 1 percent] = 35 and 31+42=39, the odds of success were somewhere in the 35-39% range. Consulting your chart this is an underestimates by 4% at the bound of the range, with the true odds being 43%.
Its super neat that you did this for exploding dice. And its really cool to see that I was on the right path

Great work!

[Telnoratti]

Your spreadsheet is actually quite clever. I didn’t even know the COMBIN function existed in excel. I think if I were to try it in excel I would have ended up with several spreadsheets. I made the same observation about coin flips and just use distributions for weighted coin flips to do other shades.

I have updated the site, improving visuals, optimizing the calculations to run faster, and including Saving Grace odds and Luck on open-ended skills. I decided that Saving Grace is used before Luck rerolls a failure which is slightly better. I also wrote a battery of tests against a simulator that takes a few minutes to run, but verified that the calculations are correct across 1,584 different results. That was necessary when I worked out the formulas for Saving Grace and Luck on an open-ended skill as the calculations were quite difficult for me and took me a while to get right. I consider it done at this point unless someone suggests visual improvements.

I’ve made some observations about Artha using my tool that people may already know or have intuitions about. First if your obstacle is one above your skill (Ob 5, B4), you have a higher chance using Luck to open-end than Boon to add a die if you have at least B3 (though both at the same time is best of course). Below that the opposite is true. Open-ending is also more efficient than shade shifting with Aristeia to reach the upper limit of your skills. B6 against Ob 6 have equivalent odds for shade shifting and open-ending. The best is Divine Inspiration, but it couples with Saving Grace very well. B5 Ob 10, with both Divine Inspiration and Saving Grace has a 50% of success (60% for open-ended). This is quadrupling the expected value!

For ensuring you succeed at lower and middle range obstacles, Divine Inspiration is best followed by Saving Grace, then Aristeia. So use Aristeia when you have a series of tests you don’t want to fail, but consider saving your Deed point for Divine Inspiration if you just have one test. If you have multiple deeds you may spend in a scene don’t forget about the power of Divine Inspiration and Saving Grace together.

Luck to open-end a skill scales very well as the exponent gets higher, but doesn’t have nearly the same impact to reroll a die for open-ended skills, dropping off past B5.

[helstadt]

This is a fantastic tool! I had been using the tables from the MoBu, but having a chart for odds with fate is just fantastic. It’s really nice having the odds of success with a call on calculated, even if it isn’t immediately obvious that you need to select saving grace to see that. It probably wouldn’t ever matter, but I realized there is one variation on dice odds that isn’t accounted for. If you have both a call-on and a deeds point, you can get the effect of saving grace twice.

[Telnoratti]

That’s a good point about Call-Ons and Saving Grace. I put a note in the interface so it’s clear that option can work for both. I can solve for two rerolls without too much trouble now that I have one working. Once that’s done I’ll just add separate checkbox for Call-Ons so that you can see the effect from both.

I don’t have a copy of MoBu, what’s the table you’re referring to?

[helstadt]

Pages 34, 35, and 36